이번 글에서는 반도체공학에서 중요한 개념인 모빌리티와 캐리어의 움직임인 drift, diffusion, recombination-generation에 대해 알아보겠습니다.
drift는 전기장 내에서 캐리어의 움직임입니다. 익히 알고 있는 분들도 계시겠지만 홀은 전기장을 따라 이동하게 되고, 전자는 전기장의 반대 방향으로 움직이게 됩니다. 하지만 반도체 안에서 격자구조를 하고 있는 실리콘 분자들이 존재하기 때문에 이들의 방해를 받으며 전기장의 영향을 받아 움직입니다. 이런 방해를 scattering이라고 부릅니다. 그래서 이러한 scattering 까지 고려한 평균적인 캐리어의 속도를 drift velocity, vd 라고 합니다.
그리고 이러한 drift 현상에 의해 캐리어가 움직일 때 생기는 전류를 drift current라고 하는데요. 전류의 정의가 단위 시간 당 흐르는 전하량입니다. 앞서 언급했던 drift velocity와 시간 t를 곱하면 캐리어의 이동거리가 나오게 되고 거기에 캐리어가 통과하는 면적 A를 곱하여 반도체 부피 안에 있는 캐리어의 수를 나타낼 수 있습니다. 여기에 저번 글에서 배웠던 홀의 수 p를 곱하면 t초 동안 한 축을 따라 이동하는 홀의 수가 나오게 됩니다. 전하량인 q를 곱하면 t시간 동안 축을 따라 이동하는 전하량이 나오게 되는거죠. 전류의 정의에 따라 시간당 흐르는 전하량을 구하기 위해 t를 나누면 아래와 같은 공식이 나오게 되죠.

여기서 전류밀도 J를 구하기 위해 면적인 A를 나눠주면 아래와 같은 식이 나옵니다.

그렇다면 모빌리티는 무엇일까? 모빌리티는 반도체의 속도에 관한 중요한 파라미터입니다. 드리프트에 의해 흐르는 캐리어의 속도에 관한 파라미터이기도 하구요. 단위는 [cm^2/V*s]이고 기호는 아래와 같습니다.

보통 실리콘 전자의 모빌리티가 1400정도 저마늄이 3900, 갈륨아세나이드가 8500정도입니다. 반도체의 고속 동작을 위해서는 저마늄이 실리콘보다 모빌리티가 높으니 더 유리한 측면이 있다는 뜻이죠. 그래서 저마늄 소재는 최신 CMOS 프로세스에 적용되고 있다고 합니다.
모빌리티가 일반적으로 움직임의 자율성을 나타내는 파라미터라고 생각할 수 있다면, 앞서 언급한 캐리어의 움직임을 방해하는 scattering의 영향을 받을 수 밖에 없습니다. scattering에는 크게 두 가지의 메카니즘이 있는데요.
1. Lattice scattering
2. impurity scattering
위 두 가지로 볼 수 있습니다. 1번은 쉽게 생각하면 자유 분방하게 움직이는 캐리어가 실리콘 격자구조에 부딪히면서 나타나는 scattering이라고 생각할 수 있습니다. 공식으로도 표현할 수 있는데요, 격자구조에 한 번 부딪혔다가 전기장을 타고 조금 더 이동하다가 한번 더 부딪혔을 때 이 부딪히기 사이의 시간을 타우라고 하면 아래와 같은 공식으로 모빌리티를 나타낼 수 있습니다.

여기서 m하고 별표 되어있는 기호는 캐리어의 effective mass, 즉 질량을 뜻합니다. 캐리어가 격자구조에 부딪히기 전 자유롭게 움직이는 시간이 길면 길수록 모빌리티가 커진다는 것이죠.
그리고 2번인 impurity scattering은 이온의 인력에 의한 scatteing입니다. 예를 들어 액셉터인 보론이 도핑되었다고 가정합시다. 전자를 흡수하고 -극성을 띄는 보론이온과 떠다니는 자유전자 캐리어가 만나게 되면 척력에 의해 밀어내겠죠? 그러면 자유전자의 궤도가 휘게 되고 그만큼 전기장의 직선적인 움직임을 따라가지 못하고 방해를 받게 된다고 쉽게 생각하실 수 있습니다. 그러면 impurity scattering은 도펀트가 많으면 많을수록 심화될 것입니다. 그리고 impurity scattering에 영향을 주는 요소가 1가지 더 있는데요, 바로 온도입니다. 온도가 높으면 높을 수록 캐리어의 속도는 빨라지게 됩니다. 그러면 도펀트들을 빠르게 훑고 지나가면서 척력과 인력의 영향을 받는 시간이 줄면서 impurity scattering이 줄어들게 됩니다. 결국 이 요소들을 공식으로 나타내면 아래와 같습니다.

Vth는 열평형 속도, thermal velocity를 뜻하고 T는 절대온도입니다.
이렇게 drift부터 mobility, scattering까지 알아봤습니다. 그러면 diffusion은 무엇일까요? diffusion을 알아보기 전에 band-bending에 대해 알아보겠습니다. band-bending은 반도체 내부에 전기장이 존재할 때 에너지 밴드다이어그램 선이 휘게 되어 위치의 함수로 표현되게 되는 것입니다.
에너지 밴드에서 에너지 E= -qV (자유전자 기준)로 나타내집니다. 즉 캐리어 하나의 전기적 위치에너지를 뜻하게 되고 일정한 레퍼런스 에너지 밴드와 밴드 사이의 gap의 크기가 위치에너지의 크기가 될 수 있다는 뜻입니다. 즉 포텐셜 에너지를 아래와 같이 컨덕션 밴드의 에너지와 임의로 정한 레퍼런스 에너지와 차이로 구할 수 있다는 것입니다.

이 포텐셜 에너지 P.E. = -q*V 이므로 전위 V에 대해서 정리하면 아래와 같습니다.

전자기학 시간에 배운 공식 E=- ∇V를 이용해봅시다. 여기서 에너지 밴드 다이어그램의 x축을 1차원 위치 축으로 보고 델을 1차원 미분으로 표현하면 아래와 같은 식이 나옵니다.
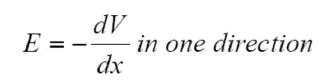
즉 E = -qV이므로 다시 쓰면 아래와 같은 최종식이 나옵니다.

이 식은 전기장이 존재하면 에너지 밴드의 미분, 즉 기울기가 존재하게 된다는 뜻입니다. 반도체 내부에 위치에 따라 변화하는 전압이 걸리면 그 기울기의 음수만큼 전기장이 생길 것이고, 그 전기장은 곧 에너지 밴드의 기울기가 된다는 ..복잡하지만 쉽게 생각하면 전기장이 있다? --> 에너지 밴드는 휜다! --> 그리고 그 휜 에너지밴드를 타고 캐리어가 이동한다 --> diffusion! 입니다.



자유전자는 그래서 저 미끄럼틀 처럼 휜 컨덕션밴드 위에 위치하게 된다면 아래 쪽으로 슝하고 미끄러지며 이동합니다. 홀은 부호가 반대이므로 밸런스밴드 아래 쪽에 놓으면 미끄럼틀을 타고 위로 올라가게 됩니다.
그렇다면 드디어 diffusion차례입니다. diffusion은 말그래도 확산입니다. 캐리어가 많은 곳에서 적은 곳으로 퍼지려는 움직임을 나타내는 말인데요.

위 그림 같이 diffusion 방식으로 캐리어가 움직이면 drift와 마찬가지로 diffusion 전류가 생기게 됩니다. 그리고 이diffusion 전류를 정의하게 된다면 fick`s law에 의해 아래와 같은 공식으로 쓸 수 있습니다.

Dp는 diffusion coefficient라는 계수이고, 델p는 위치에 따른 p의 변화입니다. 즉 캐리어가 많은 곳에서 적은 곳으로 퍼진다는 뜻이죠. 부호에 유념하셔야 되는데요. 아래 그림을 보며 설명드리겠습니다.

왼쪽 그림 기준으로 보면, 위치에 따라 캐리어의 분포가 그래프처럼 되어진다면, 전자는 많은 곳에서 적은 곳으로 확산될테니 오른쪽에서 왼쪽으로 흐를 겁니다. 그러면 전류는 반대방향인 오른쪽으로 흐르겠죠? 즉 전자가 퍼져있는 기울기가 양수임과 동시에 전류의 방향도 양수인겁니다. 따라서 둘 사이의 부호차이가 없으므로 공식에서 -가 없는거죠.
반면에 오른쪽 그림은 기울기 부호는 양수임에 반해 홀은 밀도가 작은 왼쪽, 즉 음의방향으로 흐르고 전류의 방향도 곧 음의 방향이 되어 기울기 부호와 전류의 부호가 서로 달라 -가 공식에 붙게 됩니다.
어쨌든 이렇게 해서 드리프트 전류와, 디퓨전 전류를 모두 구했는데요. 결국 총 전류는 이 둘의 합으로 나타내어집니다.
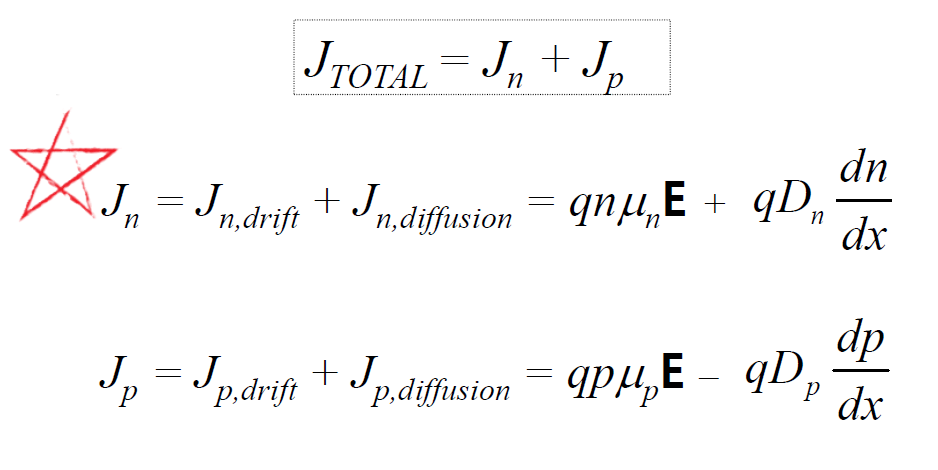
'쉬운 반도체공학' 카테고리의 다른 글
| #05 쉽지 않은 연속방정식 (1) (2) | 2021.02.03 |
|---|---|
| #4.5 쉽게 이해하는 direct 반도체와 indirect 반도체 (2) | 2021.02.01 |
| #04 쉽게 알아보는 캐리어 생성, 재결합 (4) | 2021.01.29 |
| #02 쉽게 알아 보는 페르미 함수, 상태밀도 (2) | 2021.01.21 |
| #01 반도체란? (5) | 2021.01.15 |



