저번 시간 캐리어에 대한 개념에 대해 알아봤습니다. 이번에 살펴볼 개념은 페르미 준위(레벨)이라는 개념입니다. 이 개념이 필요한 이유는 특정한 에너지 준위에서 전자의 수를 예측해볼 수 있기 때문인데요. 페르미 레벨에 들어가기 앞서 몇 가지 개념들에 대해 알아보겠습니다.
-Density Of States (DOS)
각 에너지 띠에 허용되는 상태의 수를 얘기합니다. 저번 주에 살펴본 에너지 밴드 다이어그램에서 전자는 원자가전자로서 밸런스 밴드에 있다가 밴드갭에너지 이상의 에너지를 받게 되면 컨덕션 밴드로 올라가 자유 전자가 될 수 있다고 배웠습니다. 즉 전자는 각 에너지 밴드에 위치 할 수 있고, 에너지 밴드와 밴드 사이에는 위치할 수 없습니다. 그리고 DOS는 각 에너지 밴드에 허용되는 캐리어의 자리 수라고 이해할 수 있습니다. 콘서트장 VIP구역을 에너지 밴드라고 비유하자면 VIP구역 내에 있는 좌석수를 DOS라고 비유할 수 있는 셈입니다.
그렇다면 이 DOS를 어떻게 공식으로 나타낼 수 있을까요? quantum-mechanical 공식을 푸는 것이 필요한데 학부생 과정에서 자세하게 다루지는 않았습니다. 결과만 요약해서 보여드리자면



위와 같은 복잡한 식으로 나타낼 수 있습니다. 여기서 스타가 붙은 mn과 mp는 각각 전자와 홀의 effective mass 즉 질량이라고 생각하시면 되고, 밑에 h같이 생긴 것은 플랑크 상수입니다. 그래서 에너지 밴드 다이어그램에서 이 공식에 대해 그래프를 그려보면 아래와 같습니다.
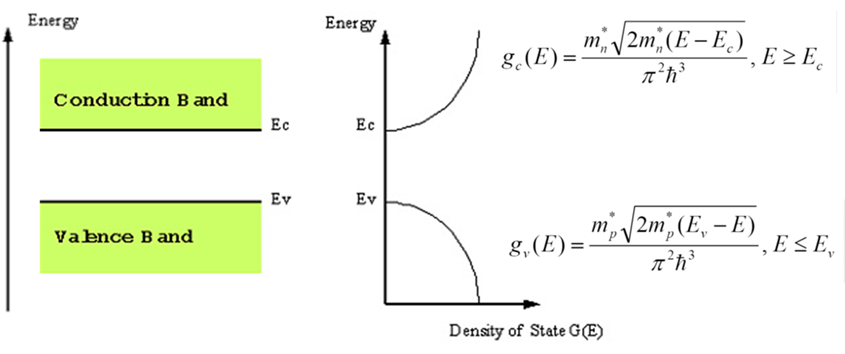
가로축이 DOS이고 세로축이 저희가 알고있는 에너지 밴드입니다. Ec 위로 컨덕션 밴드가 형성되어 있고 Ev 준위 밑으로는 밸런스 밴드가 형성 되어 있습니다. 그리고 오른쪽 그래프 같이 DOS가 에너지에 따라 점점 커지는 모습을 볼 수 있습니다. 이제 다른 한 가지 개념을 더 안다면 캐리어의 수를 유추해 낼 수 있습니다.
-Fermi Function
페르미 함수는 전자의 관점에서 전자가 그 에너지 준위에 존재할 확률을 나타냅니다. 사실 양자역학적인 관점에서 전자의 위치를 알 수 없습니다. 전자가 존재할 확률을 나타낼 뿐이죠. 그래서 이 공식은 온도와 페르미 준위라는 에너지 레벨을 알고 있다면 특정 에너지 레벨에서의 전자가 존재할 확률을 나타내줍니다. 일단 공식부터 살펴보겠습니다.

Ef는 페르미 준위이고, T는 절대온도이며, k는 볼츠만 상수(8.617*10^-5)입니다. 보통 상온에서의 절대온도를 300k라고 두게되면 kT는 약 0.026의 값을 가지게 됩니다. 그래서 페르미 함수는 0~1 사이의 값을 가지게 되는데 전자가 존재할 확률이 100%에 가까우면 1과 가까운 값을, 0%에 가까우면 0에 가까운 값을 나타나게 됩니다.
페르미 준위는 T>0K일 때, 페르미 함수의 값이 0.5, 즉 전자가 존재할 확률이 50%인 에너지 레벨을 뜻합니다. 또는 절대온도 0K에서 페르미 함수의 확률이 1인 에너지의 최대값을 뜻합니다.

T가 0K일 때 페르미 함수의 값은 산술적으로는 무한으로 치솟게 되고 최대값인 1로 나타나집니다. 이 때 1을 가지는 최대의 에너지 값을 페르미 레벨이라고 정의하는 것입니다.

다음은 T>0K에서의 페르미 함수입니다. Ef 지점에서 확률이 0.5임을 확인할 수 있고 Ef를 기준으로 +=3kT지점은 확률이 거의 1과 0에 수렴한다는 것을 확인할 수 있습니다. 만약 E= Ef +- 3kT라면 페르미 함수 공식 자체를 그래프 위에 쓰여진 저 공식으로 간략화해서 쓸 수 있는데, 이 간략화 된 공식을 볼츠만 approximation이라고 합니다. 한글 용어는 잘 모르겠네요. 그리고 온도가 만약 높은 환경이라면 위 그래프의 기울기는 완만해지고 가로로 넓어집니다. 온도가 높을 수록 원자는 다른 에너지 상태로 넘어가려는 확률이 증가하기 때문이죠.
페르미 함수가 전자 기준의 확률을 나타냈다고 했는데, 홀의 존재 확률을 구하는 방법은 간단합니다. 1-f(E)를 하면 홀의 존재 확률을 알 수 있습니다. 결국 DOS와 페르미 함수를 곱하게 되면, 캐리어의 분포를 알 수 있게됩니다. 캐리어가 존재할 수 있는 상태의 수와 캐리어의 존재확률을 곱하게 되는 것이니깐요. 그렇다면 여기서 페르미 준위의 역할은 무엇일까요? 아래 그림으로 살펴보겠습니다.

페르미 레벨이 밴드갭의 거의 가운데에 있을 때의 왼쪽부터 차례로 에너지밴드 다이어그램, DOS, 페르미 함수 (실선은 전자의 존재확률, 점선은 홀의 존재확률), 이 둘을 곱하게 된 캐리어 분포의 순입니다. 전자와 홀의 분포량이 거의 동일하다는 것을 알 수 있습니다. (사실 둘의 effective mass가 달라 정확히 같을 수 없습니다.)

위 그림은 페르미레벨이 컨덕션밴드에 가까이 위치해 있을 때 모습입니다. 페르미 함수가 위로 치우쳐 올라가기 때문에 전자의 분포가 훨씬 많아집니다.

이 그림은 페르미 레벨이 밸런스 밴드에 가까이 위치해 있을 경우입니다. 반대로 홀의 분포가 훨씬 크다는 것을 확인할 수 있습니다. 결국 페르미 준위는 미드갭을 기준으로 위 아래 치우쳐진 정도에 따라 홀과 전자의 수를 상대적으로 비교할 수 있는 척도가 된다는 것을 확인 할 수 있습니다. 즉 도핑이 없는 intrinsic semiconductor 에서는 Ef는 거의 midgap에 위치해 있을테고, 전자가 더 많은 N-semiconductor에서는 Ef는 컨덕션 밴드에 가까이 있을 것이며 P-semiconductor에서는 밸런스 밴드에 가까이 위치해 있을 것입니다.
그렇다면 전자와 홀의 개수를 알아보겠습니다. 분포까지 살펴봤으니깐 에너지 레벨에 대해서 적분하게 되면 그 수를 알 수 있겠죠. 식으로 살펴보겠습니다.

이렇게 나타낼 수 있는데, 이 식을 푸는 과정 자체가 굉장히 복잡합니다. 너무 길어질 것 같고 저도 모든 과정을 이해하는 것이 아니기 때문에 결론으로 넘어가겠습니다.

굉장히 간단하게 표현되었습니다. Nc와 Nv는 effective DOS를 나타내고 뒤에 붙은 식은 위에서 언급했던 볼츠만 approximation된 페르미 함수와 유사합니다. 이 식의 조건은 non-degenerated 와 equillibrium 상태입니다. non-degerated의 의미는 Ec-3kT>Ef, Ev+3kT<Ef 상황을 말하고, 이 상황일 때 이 공식이 유효합니다. equillibrim은 열평형 상태라는 뜻으로 흔히 반도체 공학에서는 전기장이 없는 상황을 의미합니다.
그리고 intrinsic semiconductor 상황에서 이 공식을 다른 방법으로 나타낼 수 있습니다. n=p=ni, Ef=Ei인 상황에서 말이죠.

intrinsic 상태에서의 n과 p를 구하는 공식이고, np= ni^2을 만족하는 것을 알 수 있습니다. Nc와 Nv가 들어간 공식을 이용해 ni를 구해보면 아래와 같은 식이 나옵니다.

여기서 Eg는 Ec-Ev로 밴드갭에너지를 뜻합니다.
'쉬운 반도체공학' 카테고리의 다른 글
| #05 쉽지 않은 연속방정식 (1) (2) | 2021.02.03 |
|---|---|
| #4.5 쉽게 이해하는 direct 반도체와 indirect 반도체 (2) | 2021.02.01 |
| #04 쉽게 알아보는 캐리어 생성, 재결합 (4) | 2021.01.29 |
| #03 쉽게 배우는 확산 전류, 드리프트 전류, 모빌리티 (3) | 2021.01.26 |
| #01 반도체란? (5) | 2021.01.15 |



