지금까지 드리프트와 디퓨전 전류에의한 캐리어의 변화, R-G에 의한 변화, 그리고 빛에 의한 변화까지 살펴보았습니다. 이 요소들을 종합하면 캐리어의 연속방정식을 구할 수 있습니다.

이 요소들에 의해서 캐리어는 공간적, 그리고 시간적인 연속성을 띄게 됩니다. 이 요소들을 제외하고 갑자기 캐리어가 사라지거나 나타나는 경우는 일어나지 않는다는 것이죠.
이 공식에서 나아가 드리프트와 디퓨전 전류 term을 묶어서 표현할 수 있습니다.
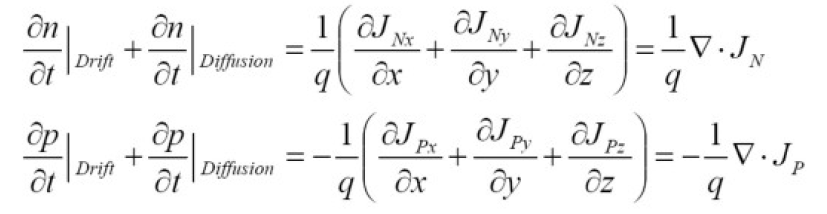
3차원 공간에서 전류 밀도의 변화량으로 나타낸 것입니다.

결국 이렇게 나타낼 수 있는데 여기서 몇가지 의문이 생길 수 있습니다. 결국 알고자 하는 것은 특정한 시간, 위치에서의 캐리어 농도인데, 이 식을 가지고 어떻게 구하냐는 것이죠. 몇 가지 가정을 하여, 디퓨전에 의한 소수 캐리어 농도를 구할 수 있는 식을 유도하겠습니다. 아래 가정들을 살펴 보겠습니다.
1. 반도체 위치는 1차원 x좌표를 통해 표현합니다.
2. 소수 캐리어들로 식을 풀어나갈 것입니다.
(저번 포스팅에서 처럼 low-level 도핑된 반도체에서 다수 캐리어는 거의 변하지 않고 소수 캐리어는 급격하게 변하기 때문입니다.)
3. 반도체에 가해지는 전기장은 0입니다.
(디퓨전에 의한 농도 변화를 구하려고 하기 때문입니다.)
4. equillibrium 상태에서의 소수 캐리어들은 골고루 분포 돼어있습니다.
(계산상의 편의 입니다. n0와 p0는 t에 대한 함수가 아니라 상수입니다.)
5. low-level injection 상황입니다.
6. Band-to-Band R-G보다는 거의 indirect R-G만 일어납니다.
(실리콘은 indirect 반도체 이기 때문에 indirect R-G가 대부분입니다.)
7. 빛에 의한 pertubation 외에 다른 외부 자극은 없습니다.
자 그러면, p-type 반도체에서 소수 캐리어인 자유전자에 대해서 식을 전개해보겠습니다.

우선 1번 가정을 통해 3차원이 아닌 1차원으로 전류밀도의 변화량을 표현합니다.

그리고 2번과 3번 가정을 통해 E=0이므로 드리프트 전류에 의한 term은 지우고, 소수 캐리어인 n으로 공식을 적었습니다.

n= n0 + Δn이므로 식을 분리해서 씁니다만, 4번 가정에 따라 n0는 상수이므로 미분값이 0이니 지워줍니다.
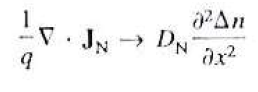
결국 위에서 정리한 식을 토대로 이렇게 나오게 됩니다.

저번 포스팅에서 구했던 R-G에 의한 변화량은 low-level injection, R-G center를 바탕으로 도출해냈으므로 그대로 불러오겠습니다.

그리고 다른 외부 pertubation은 photogeneration만 가정하고 식을 가져오겠습니다.

이렇게 위에서 가정한 내용을 바탕으로 식을 종합해보면 아래와 같습니다.
위에 식은 p형 반도체에서 소수 캐리어인 전자의 concentration을 알 수 있는 식이고, 아래 식은 n형 반도체에서 소수 캐리어인 홀의 concentration을 구할 수 있는 식입니다. 몇 가지 가정을 통해 소수 캐리어가 디퓨전에 의해 변하는 캐리어 농도를 구할 수 있는 식인거죠.
이 식은 상황에 따라 더 압축될 수 있습니다.
steady state --> 캐리어의 R-G가 일어나지만 똑같이 발생하기 때문에 캐리어의 숫자가 변하지 않고 유도되는 상황입니다. 이렇게 되면 위 식의 좌변이 0이 되겠죠.
위치에 따른 농도 변화량이 없거나 디퓨전 전류가 없다. --> 식 우변에 있는 디퓨전 전류 term이 0이 되겠죠.
drift 전류가 없거나 전기장이 0이다. --> 이미 가정한 상황이라서 이 식에 관련된 term이 없습니다.
R-G가 없다. --> 저번 시간에 구했던 캐리어 수명인 타우가 포함된 가운데 term이 0이 되겠죠.
빛이 없다. --> GL을 0으로 두면 됩니다.
그러면 문제 1개 정도만 풀이해보겠습니다.

이렇게 문제가 주어졌습니다. 골고루 도너 도핑된 실리콘 웨이퍼에 t=0인 시점에 빛이 쬐어졌고, 시간 당 10^17/cm^3의 전자와 홀들이 반도체 부피 전체에서 골고루 생긴다고 합니다. 여기서 식을 더 줄일 수 있습니다.
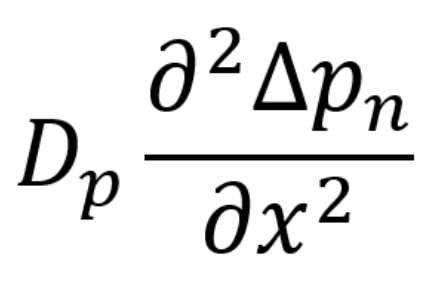
이 부분이 0이되는 것이죠. 왜냐하면 빛에 의해 생긴 Δp는 반도체 위치에 따라 달라지는 값이 아니라 골고루 생겨났기 때문입니다. 이 term을 지우고 시작합니다.
그리고 GL이 시간당 생기는 캐리어의 비율이기 때문에 캐리어 수명 시간인 타우를 곱해줍니다. 그러면 실제로 빛에 의해 발생하는 캐리어의 최대 숫자를 구할 수 있겠죠, 그러면 10^11/cm^3이 나옵니다. 도너의 숫자인 10^15/cm^3보다 한참 작기에 Δn은 무시할 수 있는 숫자입니다. 반면에 p0 = 10^9 /cm^3이기에 Δp가 100배 이상 크기 때문에 무시할 수 없습니다. low level injection인 상황에서 소수 캐리어만 다루는 이유죠. 다수 캐리어의 수는 변함이 없기 때문에 이렇게 복잡한 방정식으로 다룰 필요가 없는 겁니다.

이렇게 지울거 지우면 이런 식이 나옵니다. 미분방정식인데 미분방정식을 푸는데 필요한 경계조건을 한 개 구할 수 있습니다. 문제에서 t=0초에 빛을 쐬주면서 캐리어가 변한다고 나왔는데 그러면 그전 상황에서는 Δn, Δp = 0인데 t=0 이후에 그 변화량이 생긴다고 볼 수 있습니다. 따라서 ΔPn(0)=0 이라고 볼 수 있습니다.
그러면 이 경계조건을 가지고 ΔPn에 대해서 미분 방정식을 풀어주게 되면

위와 같은 식이 나오게 됩니다. 식으로 보면 잘 상상이 안가지만 아래 그래프를 보면서 정성적인 해석도 가능합니다.
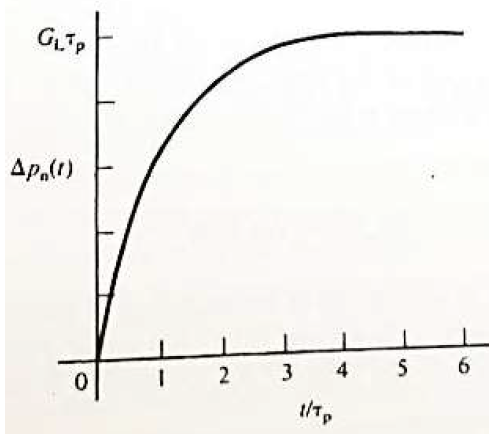
빛에 의한 pertubation으로 소수 캐리어인 홀이 가파르게 증가합니다. 홀이 generation된 만큼 R-G center에 의한 recombination rate도 증가하게 됩니다. 저번 포스팅에서 나왔듯이 recombination rate은 트랩에 있는 전자의 수도 중요하지만 밸런스 밴드에 홀이 많이 있어야 높아질 수 있으니깐요. 결국 빛에 의한 생성 vs center 재결합 간의 밸런싱이 맞춰지면서 앞서 구했던 최대 생성될 수 있는 캐리어의 수 인 GL*(캐리어 수명)로 수렴하게 되는 그래프 모양인 셈입니다.
'쉬운 반도체공학' 카테고리의 다른 글
| #08 쉽게 배우는 PN접합 (1) (2) | 2021.02.11 |
|---|---|
| #07 쉽게 배우는 준페르미준위 quasi-Fermi level (1) | 2021.02.07 |
| #05 쉽지 않은 연속방정식 (1) (2) | 2021.02.03 |
| #4.5 쉽게 이해하는 direct 반도체와 indirect 반도체 (2) | 2021.02.01 |
| #04 쉽게 알아보는 캐리어 생성, 재결합 (4) | 2021.01.29 |



