
PN접합은 보통 N-type 웨이퍼에 P형 도펀트를 도핑하여 만들어집니다. 따라서 도핑을 시작해 준 곳에는 Na(Accepter)가 훨씬 많을 것이고 점점 벌크 쪽으로 들어갈 수록 홀과 전자가 recombination되면서 그 비중이 줄어들다가 Na-Nd=0인 지점이 생기게 됩니다. 이 부분을 PN junction이라고 부릅니다. 그리고 그 부분을 지나 벌크 쪽으로 들어가면 다시 Nd가 많아집니다. 그림으로 보겠습니다.

도핑을 시작해준 곳을 x=0이라고 두었을 때 P형 도핑이 이루어져 Na의 수가 훨씬 많은 것을 알 수 있습니다. diffusion을 통해 액셉터가 벌크 쪽으로 흐르면 Nd와 합쳐져 Nd-Na =0 인 지점인 PN junction이 나오게 되고, 벌크 쪽에는 원래 N형 웨이퍼의 Nd만큼 캐리어가 존재하게 되는 형식인거죠.
그렇다면 Nd-Na를 하나의 파라미터로 볼 수 있습니다. Net Doping이라고 하는데요. x=0부근에는 넷도핑>0 일테고, PN junction 부분에서는 넷도핑이 0, 벌크 쪽은 넷도핑<0 이 되겠습니다. 그래서 x와 넷도핑을 그래프로 나타낸것을 Doping Profile이라고도 부르는데요. 대표적으로 두 가지 형식의 도핑 프로필을 꼽을 수 있습니다. Step-Junction 프로필과, Linearly graded profile 인데요. 그림으로 보겠습니다.

step junction은 웨이퍼가 라이트하게 도핑된 상태라고 생각하시면 되고, lineary graded profile은 상대적으로 헤비한 n형 웨이퍼라고 생각하시면 됩니다. 좌측 그래프가 더 급격히 넷도핑이 증가하고, 우측은 더디게 증가한 것을 보면 유추해 볼 수 있는 사실입니다. 정량적으로 해석하기에는 step junction이 상대적으로 더 편리하게 이해가 쉽습니다.
PN접합을 1차원 직선으로 두고 위치 x를 그래프로 둔 상태로 전하밀도, 전기장, 전압 등 여러 관점에서 해석할 수 있습니다. 그러기 위해서 기본적으로 전하밀도에 대한 식을 알아야합니다. 전자기학에서 배우는 푸아송 방정식에 따르면

전하밀도는 곧 전기장의 기울기와 비례관계라는 것을 확인할 수 있습니다. 그렇다면 전하밀도는 어떻게 구할까요? 홀과 자유전자의 수와, 도펀트의 수를 통해 구할 수 있는데요. 아래와 같은 공식으로 구할 수 있습니다.
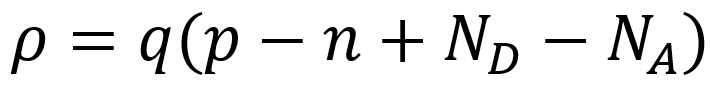
자 그러면 전기장과 전하밀도 둘 중 하나를 알면 나머지 하나를 구할 수 있고, 전기장을 알면 전압을 알 수 있게 됩니다. PN접합은 전하가 반도체 안에서 불균형하게 분포해 있기 때문에 전하밀도가 위치별로 다릅니다. 그 말은 즉 푸아송 방정식에 따라 전기장의 변화량이 위치별로 틀리다는 얘기가 됩니다. 즉 밴드다이어그램이 휘어지게 나타난다는 뜻도 되겠죠. 어쨌든 그래프로 살펴보겠습니다.

이렇게 휘어지는 걸 볼 수 있는데요 왼쪽 부분은 액샙터가 많이 분포되 있는 부분으로 페르미레벨이 밸런스 밴드와 가까이 위치해 있고, 페르미 레벨이 Ei랑 일치하고 있는 부분은 PN junction이라고 볼 수 있습니다. 그리고 벌크쪽으로 들어갈수록 넷도핑이 양수가 되며 페르미레벨이 컨덕밴드와 가까이 있는걸 확인하게 됩니다. 이렇게 컨덕션 밴드와 밸런스 밴드가 휘게 되면서 PN접합의 P부분과 N부분 사이의 전압이 발생하게 되는데요. 그림에 표시된 Vbi 전압을 built-in potential이라고 부릅니다. 에너지 E = -qV이므로 에너지 다이어 그램을 위 아래로 뒤집은 모양으로 바꾸면 전압 그래프로 나타낼 수 있습니다.
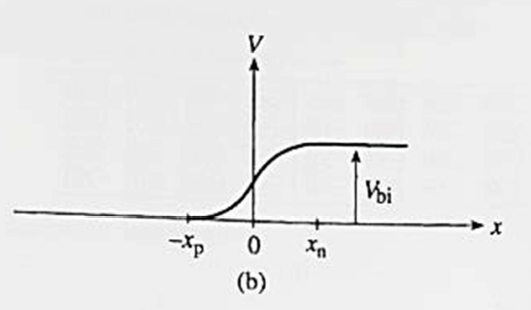
이 빌트인 포텐셜로 인해 N에서 P로 드리프트전류가 발생하게되고, P에서 N으로는 디퓨전 전류가 흐르는 메커니즘입니다. 그리고 E= -dV/dx 이므로 전기장의 그래프 또한 바로 유도가 가능하고, 전하량 역시 전기장의 기울기로 구할 수 있으므로 전하량의 그래프도 불러올 수 있습니다. 아래 그림으로 보겠습니다.

더 자세한 사항은 다음 포스팅에서 다루겠습니다.
'쉬운 반도체공학' 카테고리의 다른 글
| #10 PN접합의 전류-전압 특성 (0) | 2021.02.25 |
|---|---|
| #9 쉽게 배우는 PN 접합 (2) (0) | 2021.02.19 |
| #07 쉽게 배우는 준페르미준위 quasi-Fermi level (1) | 2021.02.07 |
| #06 쉽지않은 연속방정식(2) (2) | 2021.02.05 |
| #05 쉽지 않은 연속방정식 (1) (2) | 2021.02.03 |



